Butterfly Effect, Model Ensemble and Probabilistic Forecast
Butterfly Effect, Model Ensemble and Probabilistic Forecast
Jeffrey LEE Chi-wai
December 2012
"Does the flap of a butterfly's wings in Brazil set off a tornado in Texas?"--- Edward Lorenz, father of chaos theory and butterfly effect
This is one of the well-known quotes in the 20th century. The meaning of this quote is that for a complex system like our atmosphere, a small change in the initial stage (slight change in air flow due to a flap of butterfly's wings in Brazil) could result in a huge difference (setting off a tornado in Texas) in a later stage. This effect can be illustrated with the Lorenz Butterfly shown in figure 1. If the reader searches the keyword "Lorenz Butterfly" on the Internet, thousands of similar images will come up but it will be almost impossible to find two images that have exactly the same traces. The slight differences in the initial position of the traces that the authors used in generating the images have resulted in the subsequent differences that emerged in the path of the traces.
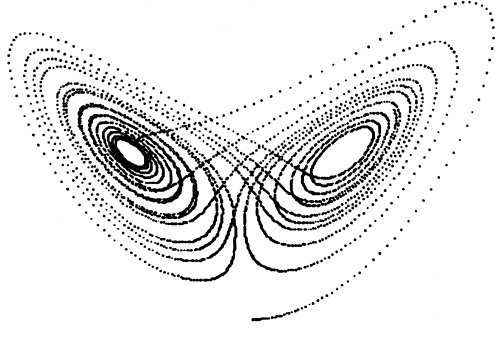
Figure 1: Lorenz butterfly - resemble a real butterfly
In the simulation of weather using a computer model, slight inaccuracies in representing the initial condition in the model could result in completely different weather forecasts in the later stages. Such inaccuracies are, however, inevitable due to the inherent inaccuracies in taking weather observations to represent the initial condition of the atmosphere. In order to tackle this problem, the meteorologists have developed a forecast technique called the "model ensemble". Model ensemble refers to the use of a number of models, each starting with a slightly different initial state, in an attempt to capture all possible scenarios of the future weather and to derive the chance of occurrence of each scenario.
One difficulty in operating a model ensemble system is the high computational cost involved. It takes a supercomputer to run a high-resolution model in an attempt to catch up with the evolution of weather in the real atmosphere. It is prohibitively expensive to run thousands of them to capture all the possible weather scenarios in the future. To overcome this difficulty, the resolution of the models has to be suitably reduced. Moreover, special mathematical techniques are applied to identify those initial variations that will more likely lead to different weather scenarios. By doing so, the number of model runs required for the model ensemble system can be reduced to a minimum. Nowadays, the model ensemble systems in operation at various big weather centres have dozens of ensemble members.
Apart from the above, the interpretation of products from model ensemble is by no means straightforward. For a model ensemble with 50 ensemble members, it may give 50 different temperature forecasts for tomorrow (to illustrate how complicated it could be, imagine that one morning you switch on the TV and find that, as shown in figure 2, 50 weather presenters to report, with each of them presenting a different forecast). One common method to present the uncertainty in the weather forecast is by way of probabilities. For example, a probabilistic forecast for the rainfall tomorrow may be presented as something like the chance of having any rainfall tomorrow is 30%. Such a message tells you that if the weather is made to evolve 100 times from similar initial condition into the future, rainfall will actually occur the following day at around 30 times of them. When compared with "the chance of having any rainfall tomorrow is 70%", one will appreciate which is more likely to have rain in the following day. The probabilistic presentation of forecasts is gradually gaining popularity among the meteorological agencies around the world.

Figure 2: "Ensemble weather report on TV"
Lets conclude with a joke: Because of the butterfly effect, reader of this article may have already accidentally seeded the formation of a typhoon somewhere on this planet by yawning during reading. Such effect may be offset by telling your friend about what you have learnt from this article and making him/her yawn too.